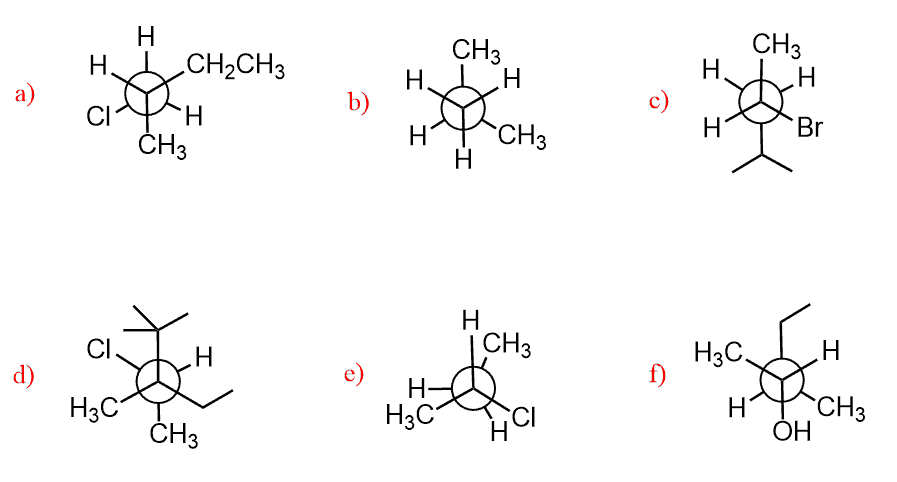
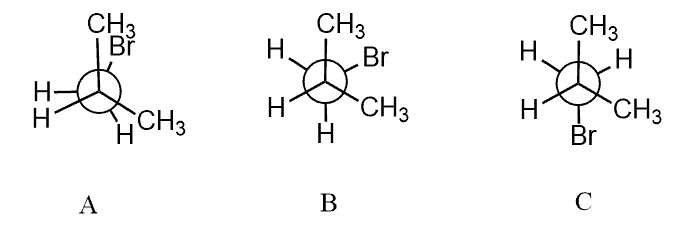
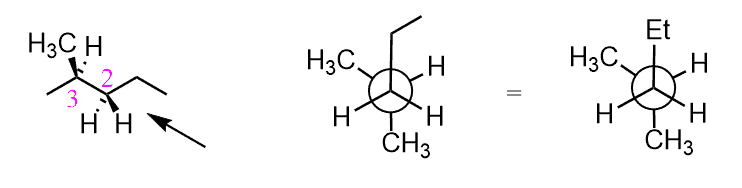
Torsional and Steric Strain
In the previous post, we talked about the Newman projections where we also covered the relative energies of anti, gauche, and syn conformations. The destabilization of certain conformations is due to Steric or Torsional strain. These two definitions are synonymous and their difference is often overlooked. This is how you can think of it:
Steric hindrance is a broad definition and it occurs when atoms or groups are close to one another and there is an increase in energy because of the repelling electron clouds.
The torsional strain, on the other hand, is specifically for the eclipsing groups as a result of repulsive forces between the bonding electrons of these groups. The increase in energy resulting from eclipsing groups on adjacent carbons is called Torsional Strain. And for this to be considered torsional strain, it needs to be an energy increase of small eclipsing groups – H/H, or H /CH3.
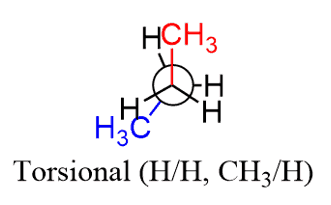
When two large groups are eclipsed, there is both torsional and steric strain:

Here is also a short video clip to visualize better the steric and torsional interactions in the eclipsed conformations of butane:
The interaction of two gauche groups is a steric hindrance. For example, gauche conformations are less stable (higher in energy) than anti conformations because of the steric strain associated with the larger groups being closer to one another (60o vs 180o).
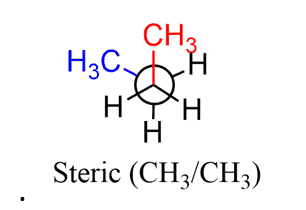
The energy values for the torsional and steric strain are summarized in Table 1:

The torsional strain is more relevant in cyclic compounds where the free rotation about single bonds is restricted. For example, there are six eclipsing hydrogens in cyclopropane, and this unfavorable tension cannot be relieved because the molecule is planar by necessity:

Notice that aside from the torsional strain, there is also a bond angle strain caused by the deviation of the bond angles from the ideal tetrahedral geometry. These two factors make the ring strain which is characteristic of small cycloalkanes. There is a separate article on ring strain which you can find here.
How to calculate the energy of conformations
Each group has its associated energy when it is at the syn or gauche position to another group. You will most likely be given the torsional and steric energies for different groups. In general, to calculate the total energy of a given conformation, add all the torsional and steric strain:
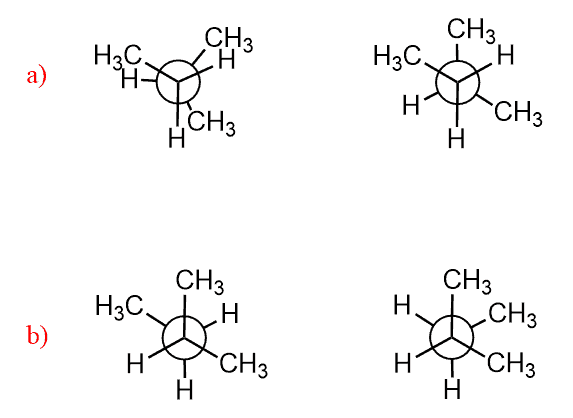
For example: Calculate the energy difference between these two conformations of butane:
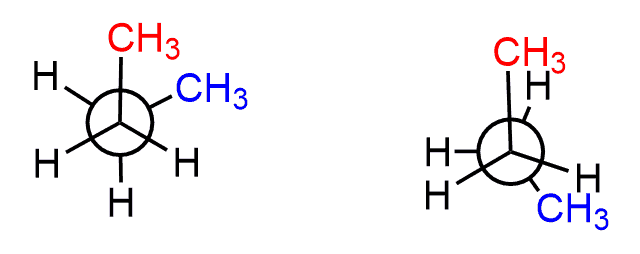
The first conformation has one CH3/CH3 gauche interaction which brings 3.8 kJ/mol energy of destabilization. The second conformation is three pairs of eclipsing groups: one H/H = 4 kJ/mol and two H/CH3 = 2 x 6 kJ/mol = 12 kJ/mol. In total, 12+4 = 16 kJ/mol.
The energy difference is 16 – 3.8 = 12.2 kJ/mol.
The following short clip of conformational analysis illustrates the conformations of butane and the energies associated with them on an energy diagram:
Check this article for more details about the Newman projections and conformations of butane.
To calculate the barrier to rotation, subtract the energy of the most stable (lowest energy) staggered conformation from the least stable (highest energy) eclipsed conformation.