Alkanes and Cycloalkanes

Newman Projection of Chair Conformation

We have learned that a Newman projection represents a molecule looking from a specified direction and a given bond. Therefore, a molecule can have multiple Newman projections depending on this bond and the direction we are looking from. For example, the anti conformation of butane is usually drawn looking through the C2-C3 bond, and it has two common Newman projections depending on the viewing angle:

 

 

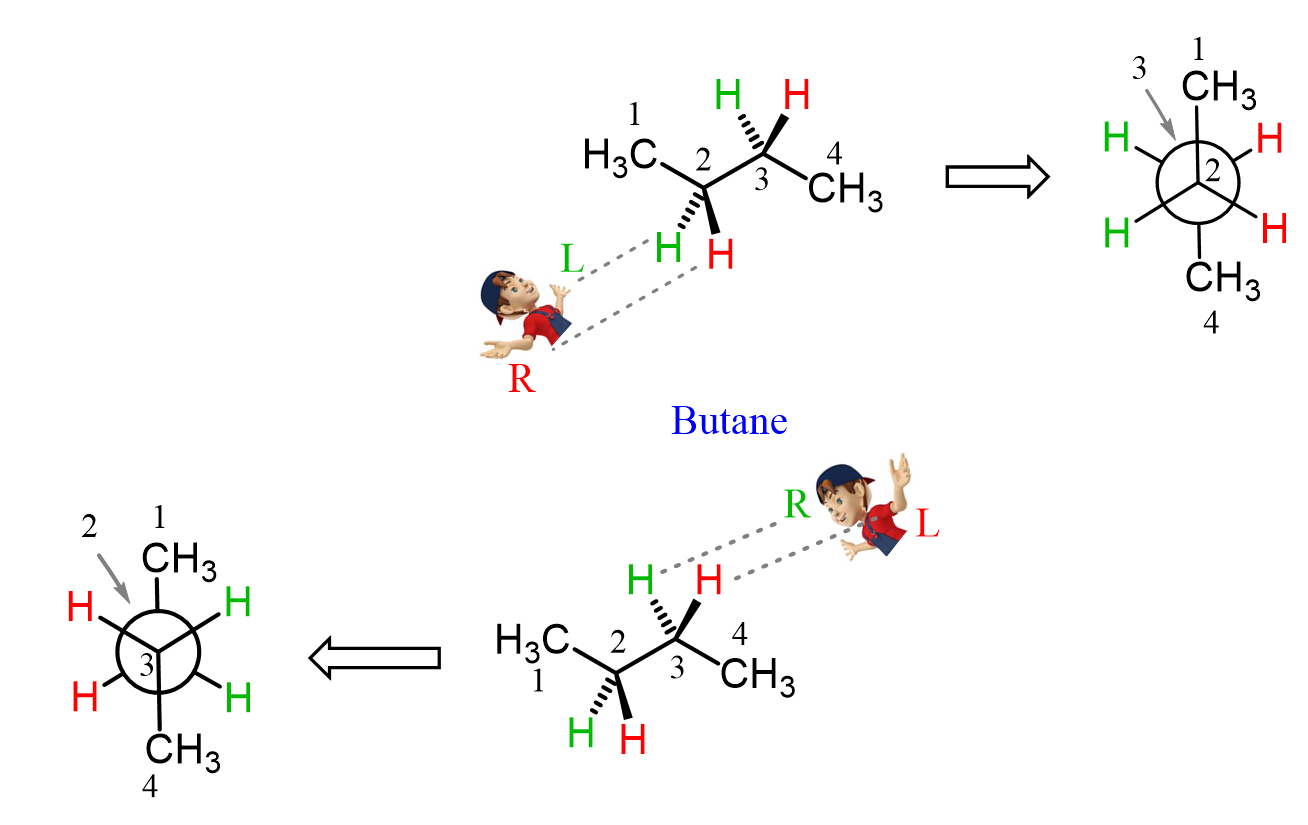
This was just a quick reminder of what Newman projections are and how they can be drawn. The key principles and strategies we use for drawing Newman projections are covered in the linked articles, so feel free to review them before we start drawing them for chair conformations of cyclohexane.

 

Newman Projection of Cyclohexane Chair

The same methods used for alkanes are also applied to draw the Newman projection of cyclohexane, and the only difference is that here we are looking through two parallel bonds. For example, let’s draw one form of the chair conformation, and highlight the bonds through which we are going to look:

 

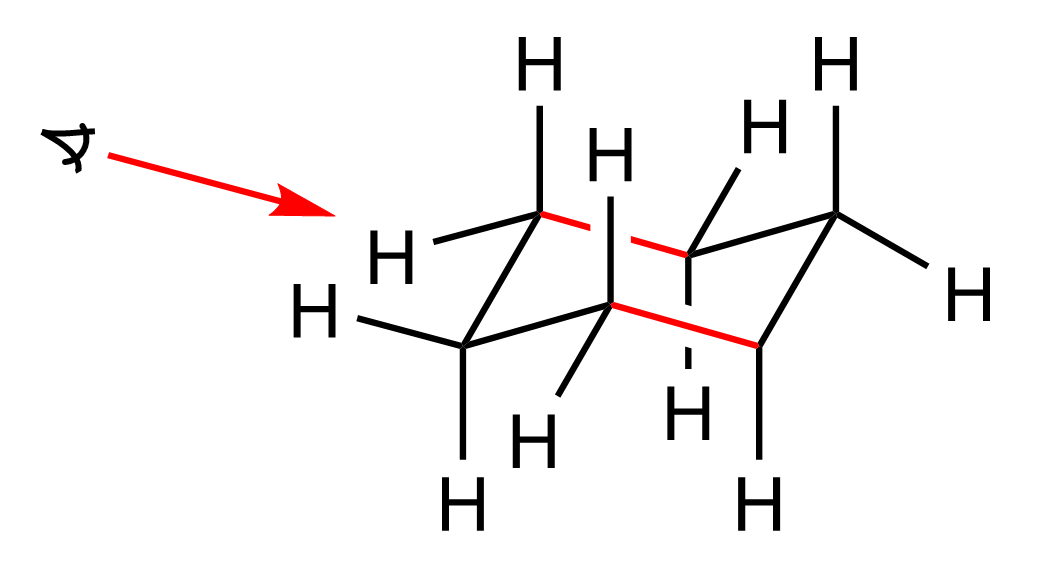
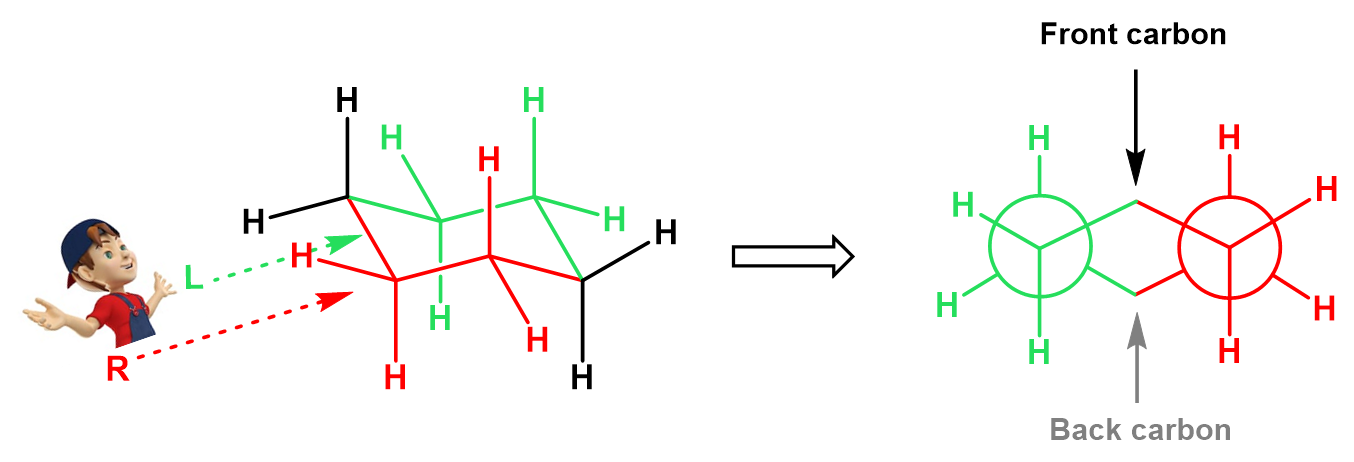
There are two bonds we are looking through, so you can visualize this as two Newman projections which are connected via the foremost left and right carbons of the ring. To illustrate this, let’s color in red the part of the ring that is closer to us, and the other half that is away from us, in green:

 

 

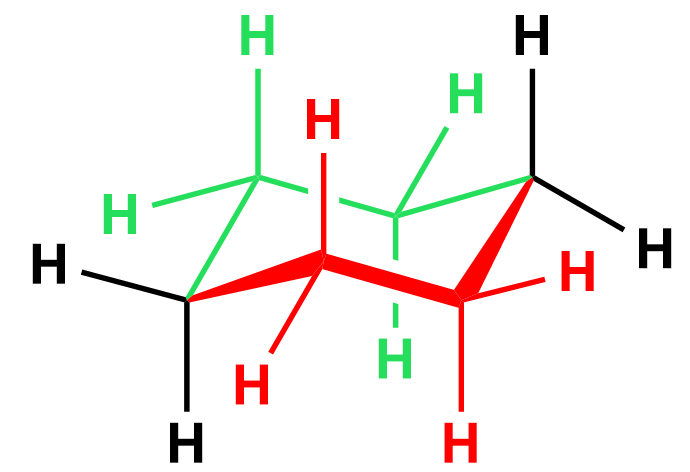
In the Newman project, looking from the top left, the red half of the ring is going to be on our right, and the green half, on our left side:

 

 

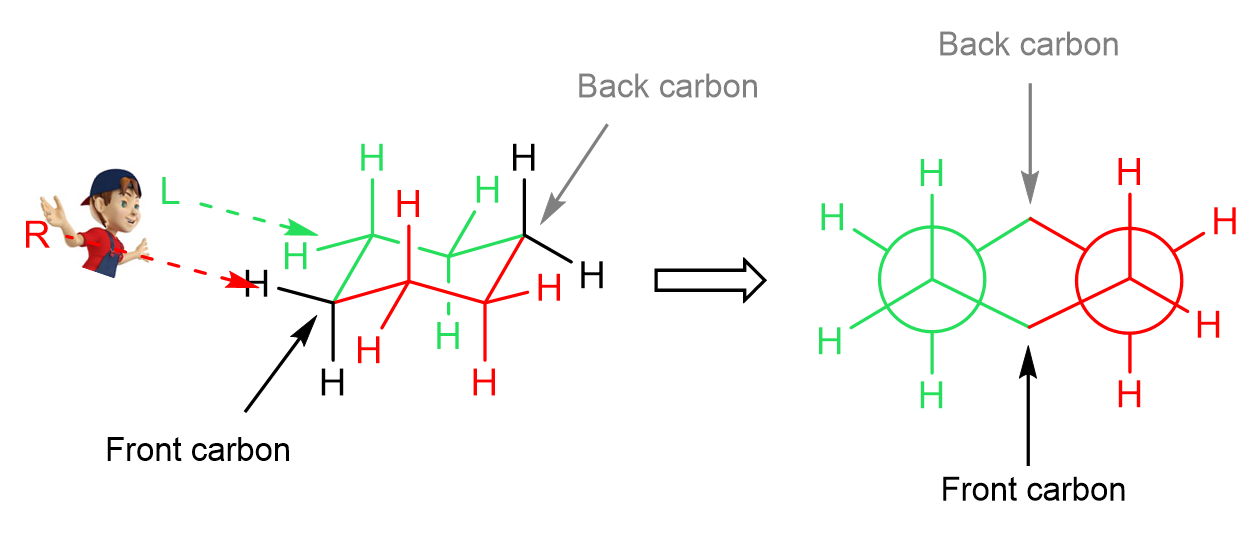
The hydrogens on the front and back carbons are emitted as they get on the way of the projection. All of this can be better seen in a 3D representation, so here is a short video clip for that:

 

Notice that the front two carbons have the upside-down Y shape and the back carbons behind the circle have the Y shape (we are talking about the carbons that are part of the bonds we are looking through).  Like in any other Newman projection, this will change if we look from the opposite side, and for cyclohexane, we can also observe this if we are looking at the other chair conformation (ring flip) from the same side:

 

 

Newman Projection of Substituted Cyclohexanes

Now that we have some idea of how the chair is converted into a Newman projection, let’s add some substituents on the ring. For example, let’s draw the Newman projection of the following cyclohexane with four groups/atoms on the carbon atoms that are part of the central bonds:

 

 

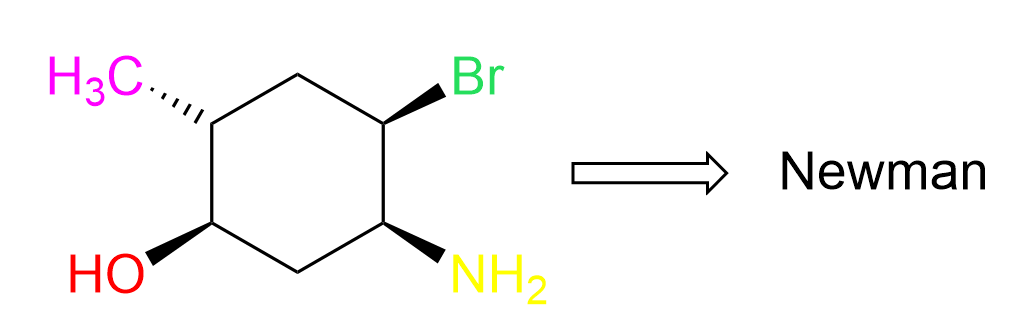
We will draw the Newman projection for each chair form looking from both angles, but first, we need to convert the structure to a chair conformation. There is a separate post showing how to convert a cyclohexane to both chair forms, but in short, this is what we need to do:

 

 

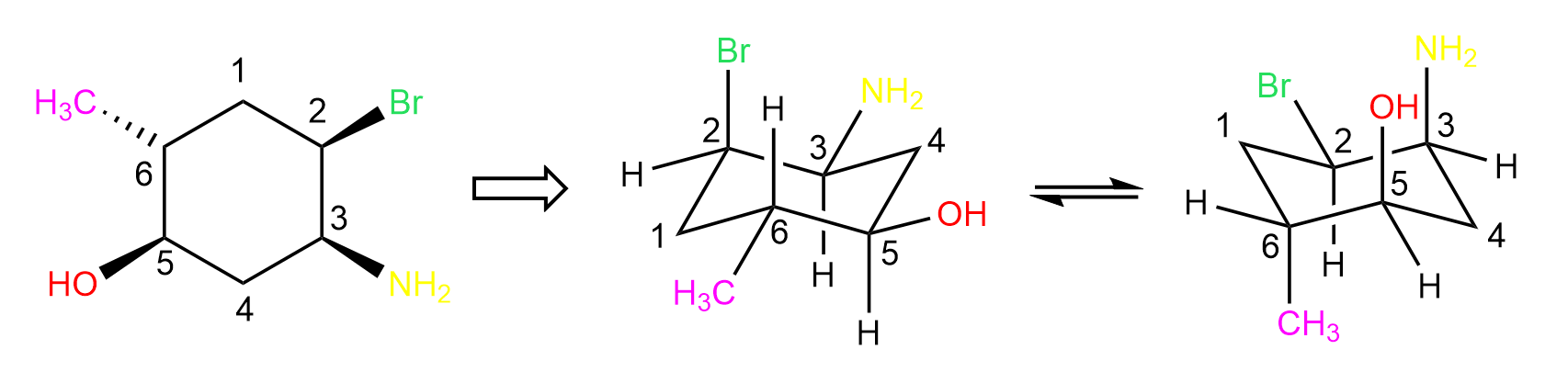
As mentioned in the summary, we start by numbering the ring, which is always a good idea in organic chemistry, and the direction does not matter at this step. So, let’s number the carbons clockwise starting from the top atom, draw one of the chair forms, add the groups/atoms, and do a ring-flip to get the other chair form:

 

 

Now we can convert the first chair structure to a Newman projection looking from the top left corner. In the front, we are going to have carbon 1, and the two carbons in front of the imaginary circle are carbon 2 and 6 on the left and right sides respectively.

 

 

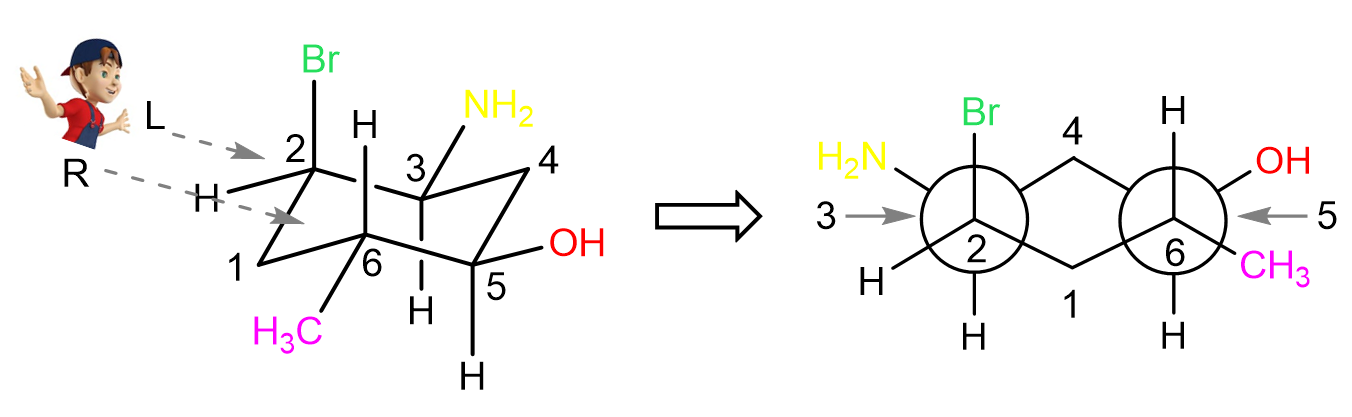
On carbon 2, we have the axial bromine pointing straight up, and on carbon 6, we have an equatorial methyl pointing outside of the ring. The two carbons behind the circles are carbon 3 and 5 and they have equatorial amino and hydroxy groups pointing outside of the ring. Carbon 4 is in the back as it is the farthest from the viewer:

 

Next, let’s see the Newman projection looking from the right side. Here, carbon 4 is pointing up and is the closest to the viewer whereas carbon 1 is the farthest from the viewer and it is pointing down:

 

 

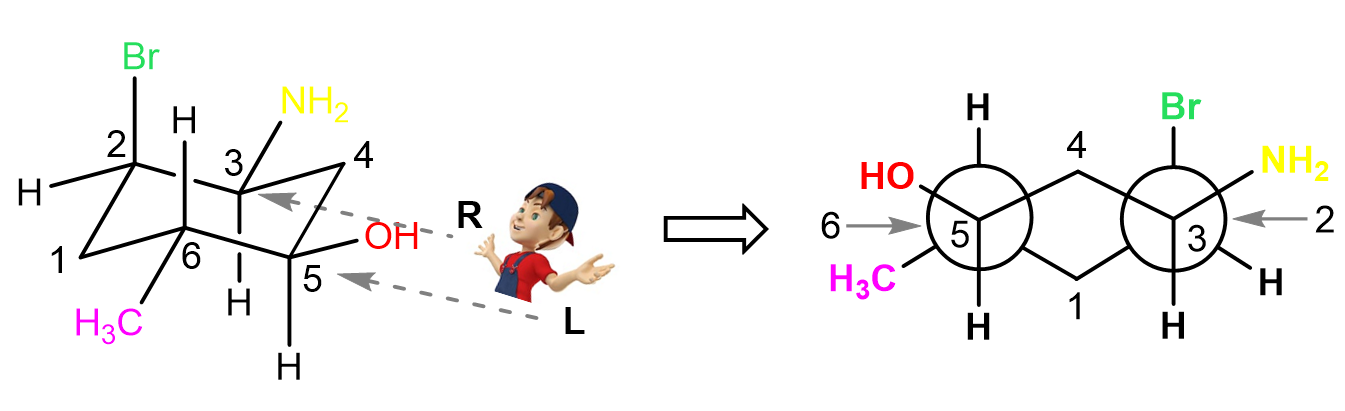
Notice that the carbons in front of the circle are now 5 and 3 and they have the OH and NH2 groups pointing outside of the ring.

 

Let’s also show the Newman projections of the second chair conformation looking from both directions. Because of the ring flip, all the groups have switched from axial to equatorial, and equatorial to axial positions. First, looking from the bottom left, we are going to have carbon 2 and 6 on the left and right sides respectively, and they both have the Y shape. The Br is pointing outside of the ring, and the methyl is now pointing straight down:

 

 

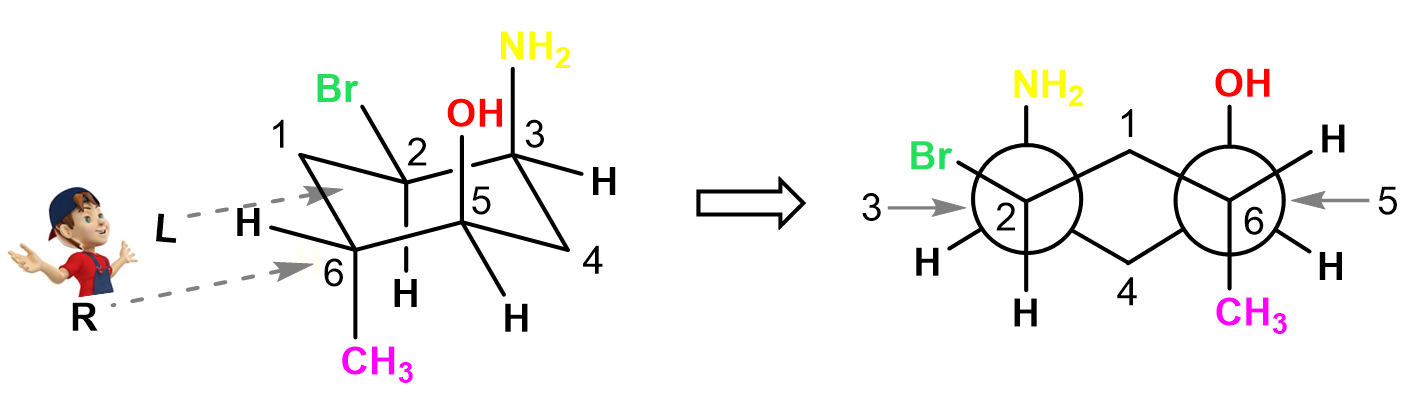
Carbon 3 and 5 are behind the circles and on those we have axial NH2 and OH groups both pointing up:

 

For the same conformation, looking from the top right side, we will have carbon 5 and 3 in upside-down Y shapes on the left and right sides respectively. On these carbons, we have the axial OH and NH2 groups pointing straight up. The two carbons behind the circle are carbon 6 and 2. On carbon 6, there is an axial methyl group pointing straight down, and on carbon 3, we have an equatorial bromine pointing outside the ring:

 

 

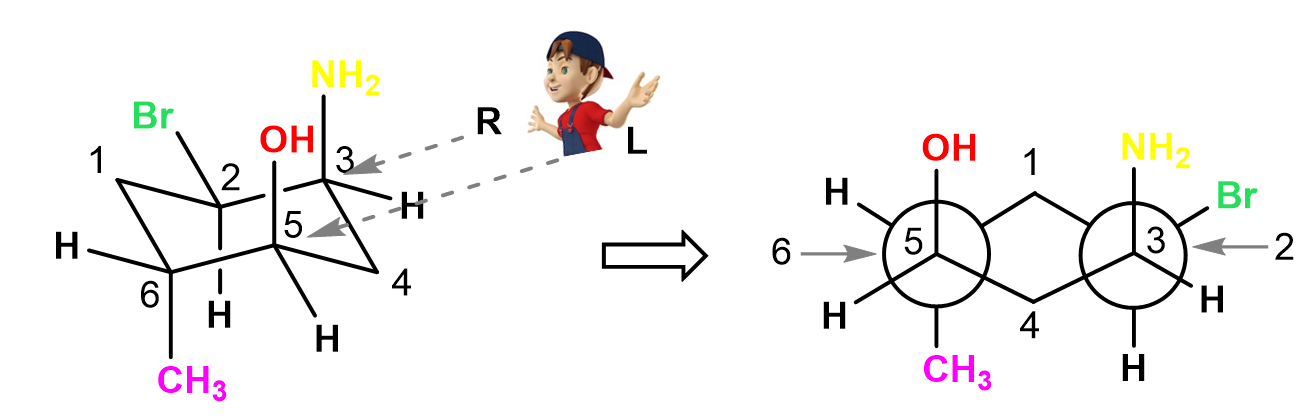
In all the examples above, there were no groups on the front and end carbons of the cyclohexane, so let’s also do one such example:

 

Let’s again number starting from the left carbon going clockwise. The first Newman projection is for the view from the top left corner:

 

 

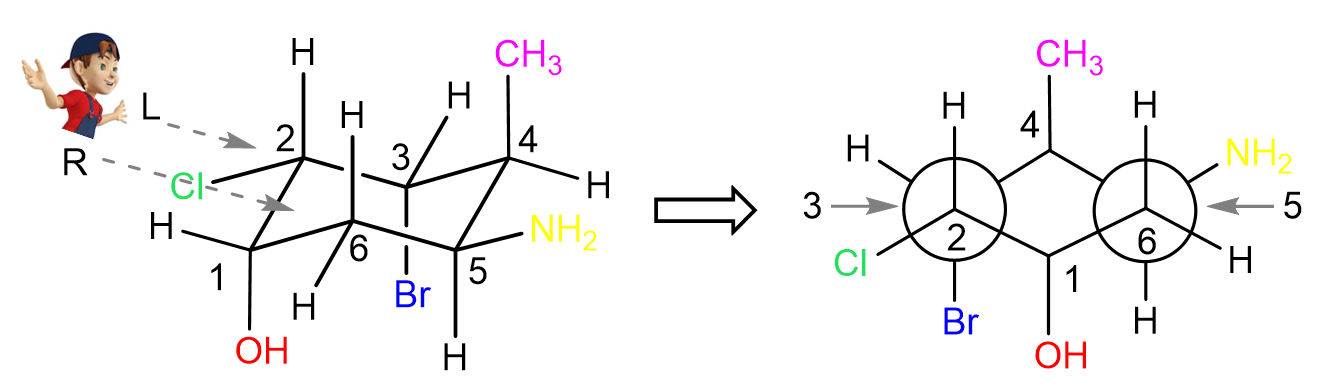
Notice that both the CH3 and OH groups are axial, thus pointing straight up and down respectively. The hydrogens on carbon 1 and 4 are still omitted because of lacking space, however, you can add them slightly pointing up or down as seen in the video representation below:

 

Converting Newman Projection to Chair Conformation

In the last part of this article, let’s also discuss the reverse process of what we have been doing. So, now, we are going to convert a Newman projection of cyclohexane to the corresponding chair conformation.

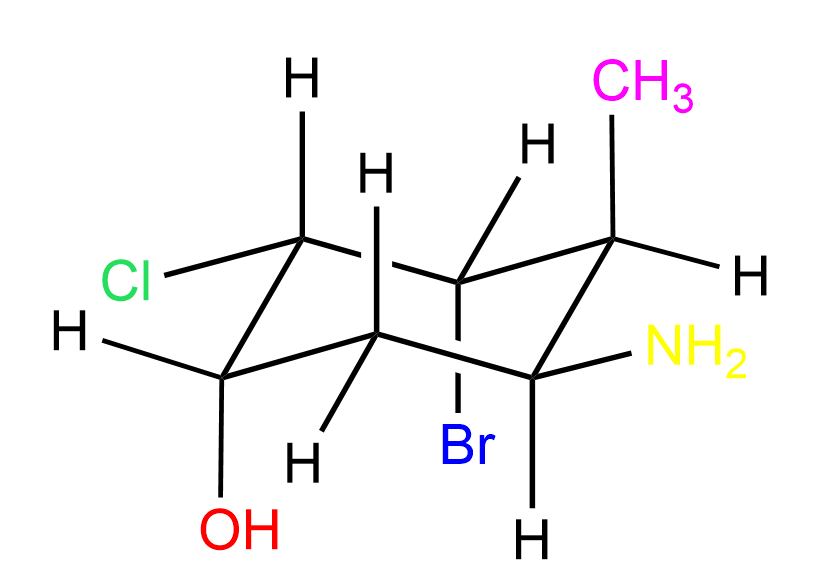
For example, convert the following Newman projection to the corresponding chair form:

 

 

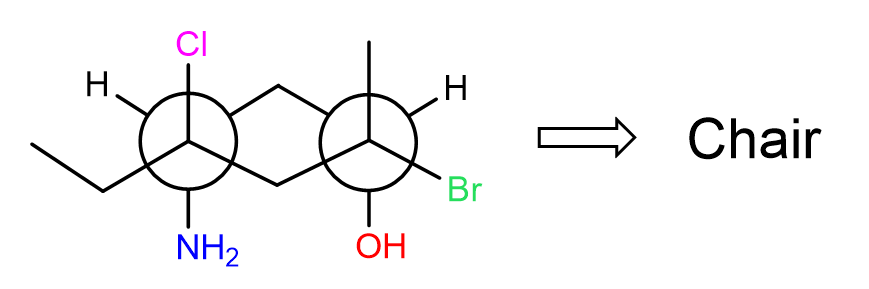
As always, start by numbering the carbons in the ring starting from the front carbon and go clockwise:

 

 

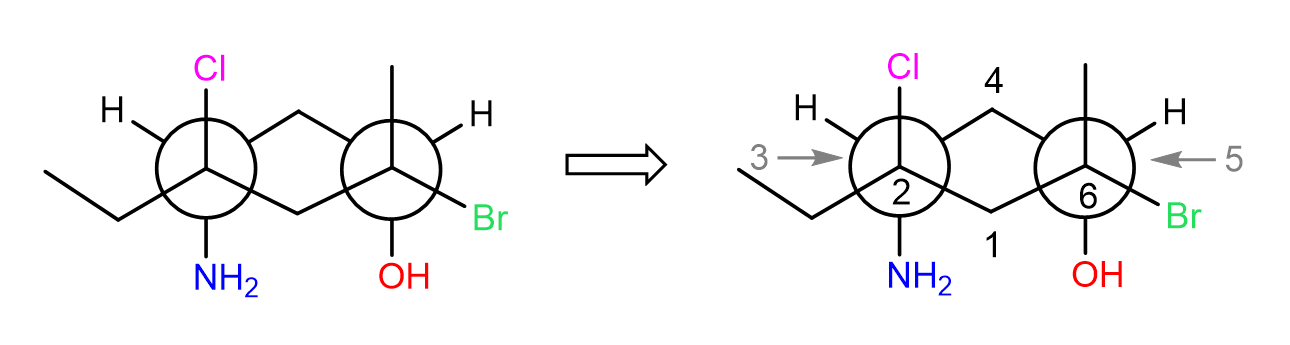
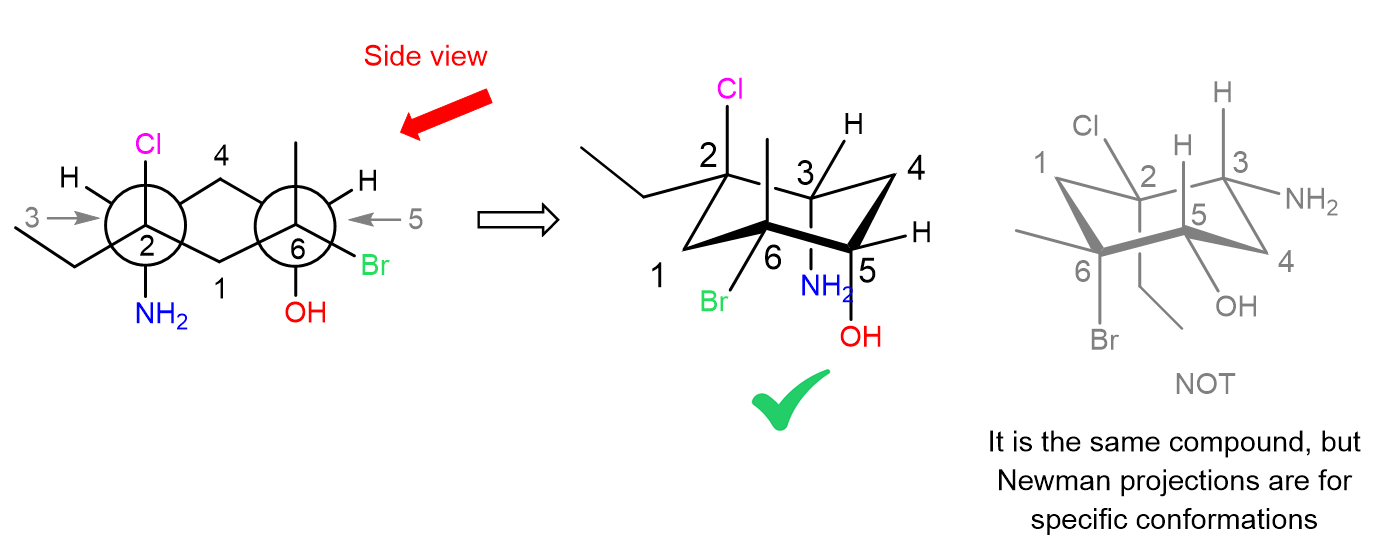
Next, we look from the side to determine the chair form of the ring. For example, looking from the right, we are going to have carbon 1 on the left, and carbon 4 on the right side of the chair. All the groups that are pointing up, must also point up, and those pointing down, must also point down in the chair conformation:

 

 

Notice also that carbon in the Newman projection is pointing down, whereas carbon 4 is pointing up, therefore, when looking from the right, we get this specific form of the chair. And even though the other conformation (ring flip) would still represent the same molecule, we need to keep in mind that a given Newman projection of the molecule is for that specific conformation:

 

Check Also

Share Your Thoughts, Ask that Question!