In the previous post, we talked about drawing the two conformations of cyclohexane (ring-flip). Remember that conformations are different arrangements of atoms originating as a result of rotation(s) abound a single bond(s). This means that the ring flip is a reversible process that at some point reaches an equilibrium. Let’s discuss methylcyclohexane as an example:

What is interesting here is that this equilibrium is not a 50% : 50% mixture of the conformations. It is shifted to the more stable chair conformation. The ratio of two chair conformations in the following mixture is 95 : 5 in favor of the one where the methyl group is equatorial. What is the reason for this?
1, 3-Diaxial Interactions
To understand this preference for chair conformations, let’s draw out the hydrogens of the methyl group and the ring:

What we notice is that the methyl at the equatorial position is pointing away from the ring and has plenty of space. On the other hand, when the methyl is axial, it lacks space (steric interaction) mainly due to the hydrogens that are also on axial pistons.
Notice also that, these groups (the axial methyl and the hydrogens) are one-carbon apart and if we number, we can see that their relative position is 1,3 and that is why it is called 1,3-diaxial interaction:

Now, one question for you:
do you see anything in common between the 1,3-diaxial interactions and gauche conformation (Newman projections)?
Or, even better – can you see that they are the same thing?!
Let’s see how that happens. If we convert the chair cyclohexane to its Newman projection, we can see that the methyl group has a gauche interaction with the CH2 group just like in butane:
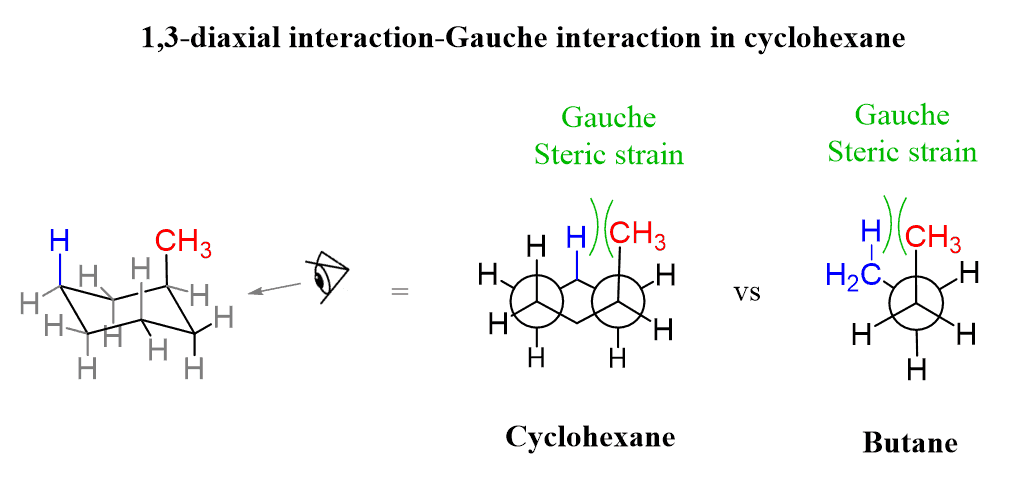
The second gauche interaction can be seen by looking from the bottom left corner:

So, the 1,3-diaxial notation is the most common way we refer to the gauche interactions of axial groups in the chair conformations. Generally, the axial conformation of a given cyclohexane is less stable than the corresponding equatorial conformation.
A values
The actual energy difference of the conformations is calculated by the Gibbs free energy formula:
ΔGo = – RT ln Keq
And using the ratio 95:5, it is calculated that this corresponds to 7.28 kJ/mol. So, the equatorial conformation is more stable than the axial by 7.28 kJ/mol. This energy difference is known as the A value and it varies depending on the axial group.
The larger the group, the higher the energy difference. For example, the energy difference of the axial ethyl cyclohexane with the equatorial conformer is 7.3 kJ/mol:
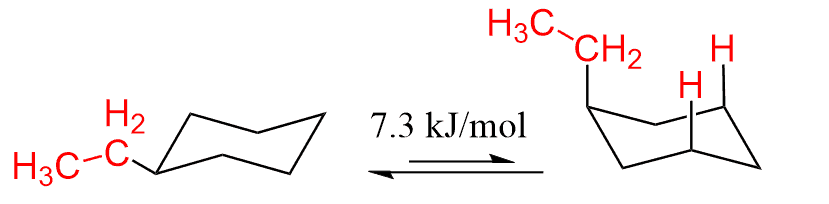
This is interesting because the ethyl group has an additional methyl and you may expect that it should bring a significant steric strain (more than 0.02 kJ). However, because of a free rotating around the single bond, the methyl points away from the ring thus reducing the steric strain:

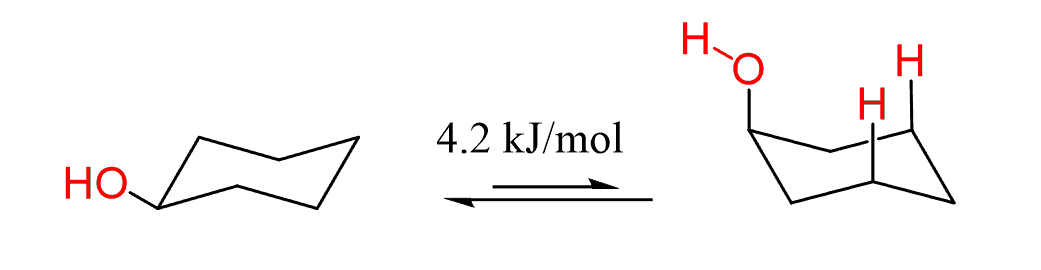
For the same reason, the hydroxyl group does not bring as much of energy change as might be expected because of the fact that oxygen is a larger atom than carbon. Since there is only one hydrogen on it, the oxygen can always rotate such that the hydrogen is pointing away from the ring minimizing the steric interactions.
The isopropyl as well, being a large group has a relatively small A value as it is able to retain the favorable conformation where the two methyl are pointing away and only the H interacts with the axial hydrogens:

In general, sp2-hybridized carbons do not have such high A values, because they are flat and can adopt a suitable conformation to reduce the steric strain: For example, benzene, being a large molecule has an A value of only 11 kJ/mol:
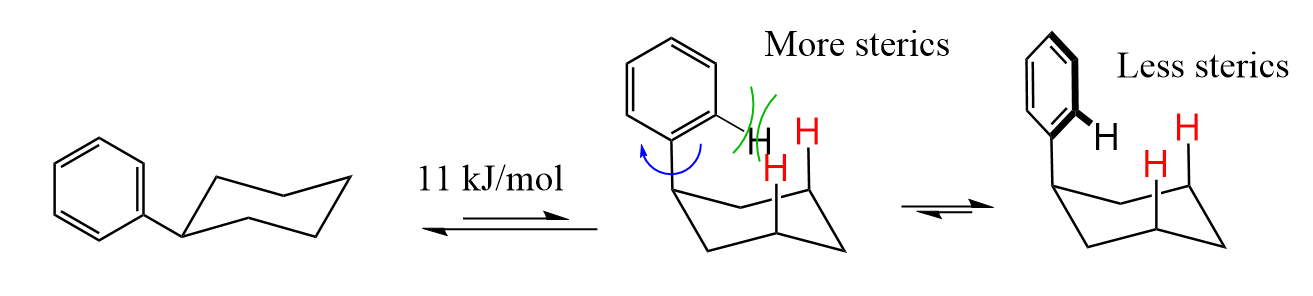
However, as we increase the number of carbon atoms on a tetrahedral center, it becomes more difficult to avoid high-energy 1,3-diaxial interactions:
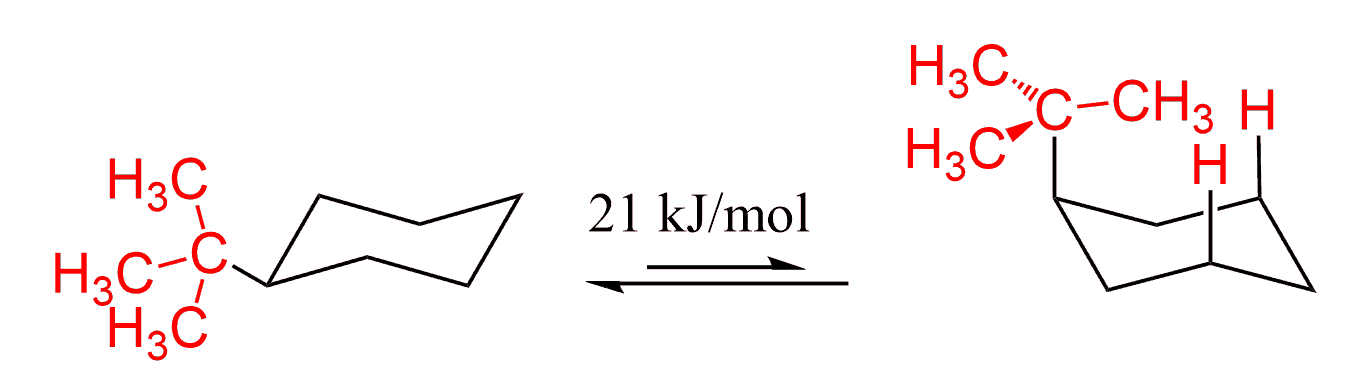
Below is the table for the A values for the axial-equatorial equilibrium of the most common substitutions:




Can I ask about the answers to the practice questions please?
Yes, please go ahead. I need to add the answers…
The answers are there – some math from Gen Chem 2 to have fun.
Why the Bromine substituent has higher energy 1,3-diaxial interaction than Iodine substituent although Iodine atom is bigger than Bromine?
Good question. One explanation can be the large size of the iodine atom because it is in the fourth row of the periodic table. The very long C-I bond may be placing iodine atom too far from the axial hydrogen atoms and decreasing the interaction.
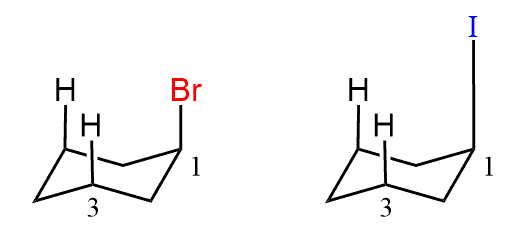
Here is an exaggerated image for a visual perspective:
Dear Dr.,
C-I bond is shorter than C-Br bond.
Please try again.
Kris
Where does it say that C-I is shorter than C-Br?
Thank you for the reply. It is helpful for understanding.
You are most welcome!
If a methyl group and chlorine are roughly the same size, why then is the A value for Cl less than that of the CH3?
Where does it say that they are approximately the same size?