Conformational analysis is the study of the relative stabilities of different conformations of a molecule. Recall that conformations or conformers are different spatial arrangements of atoms in the molecule, which are achieved as a result of rotations about single (σ) bonds.
Conformational Analysis of Ethane
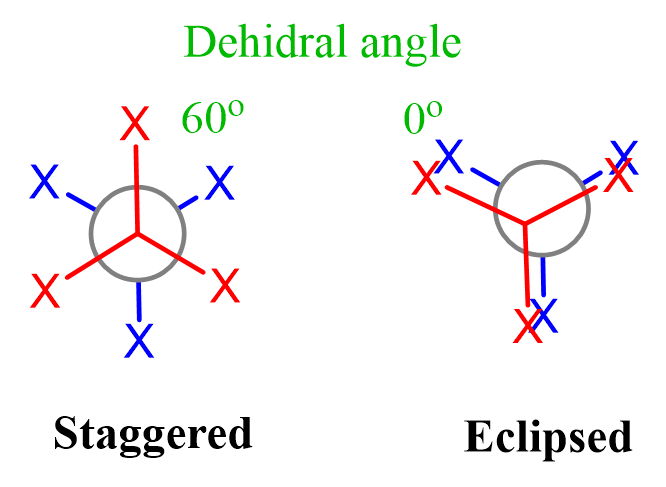
For acyclic molecules, conformations and conformational analysis are shown most often with Newman projections. For example, ethane, as a simple alkane, has only two conformations: staggered and eclipsed. In the staggered conformation, all the neighboring hydrogens are at 60o. The continuous rotation about the C-C single bond places these hydrogens at any angle; however, the other important conformation is achieved when the angle is 0o (eclipsed conformation).

The staggered and eclipsed conformations are not unique to ethane only. All the conformations of any two connected tetrahedral carbons are either staggered or eclipsed:
As we know from the conformational analysis of ethane and propane, staggered conformations are more stable than eclipsed conformations because of steric and torsional interactions.

Although quite similar and often used interchangeably, the steric torsional interactions have different definitions. Sterics or steric interactions are the obstructions caused by the size of neighboring groups and atoms. Torsional interactions are the result of repulsive forces between the bonding electrons of neighboring atoms.
Both steric and torsional interactions are observed mainly in eclipsed conformations because that is when the groups come into close proximity. The energy values of the steric and torsional interactions between H and CH3 groups are given in the table below:

For ethane, there are only hydrogens on the neighboring carbons and therefore the energy of the eclipsed conformation is due to the torsional strain between three pairs of hydrogens, which account for a total of 12 kJ/mol (2.9 kcal/mol) destabilization:
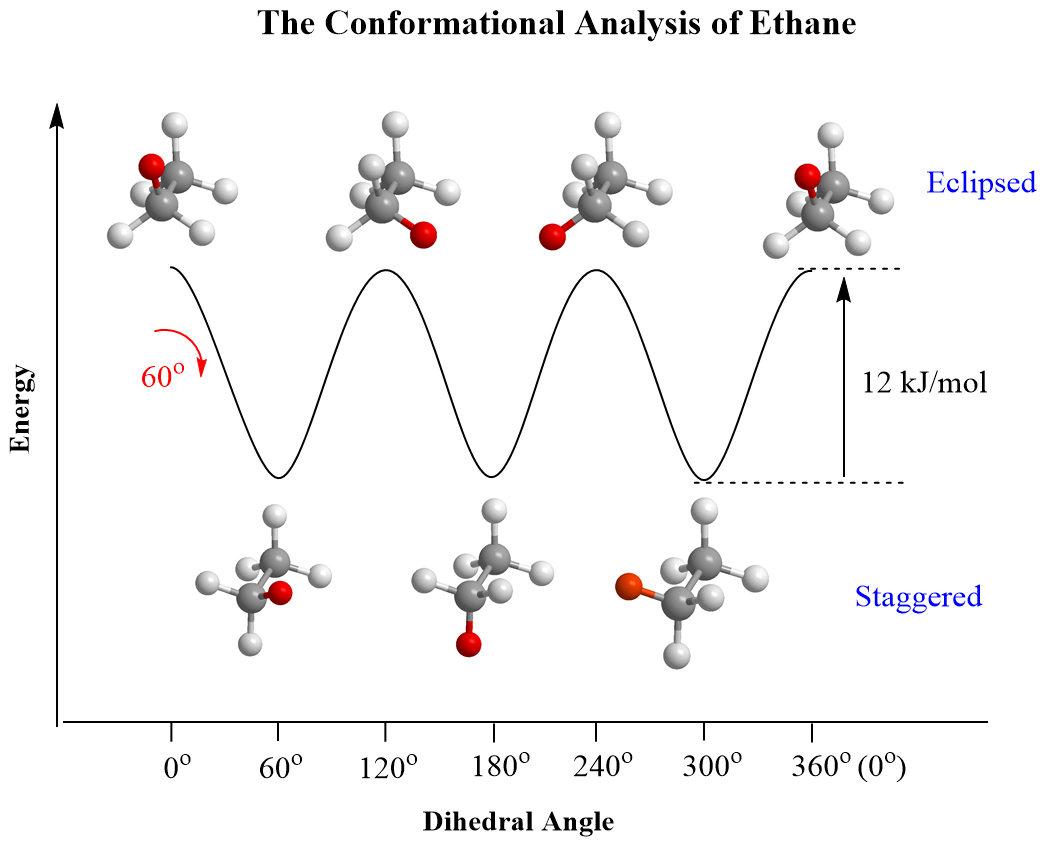
This is the barrier to rotation in ethane, which is defined as the energy difference between the most stable (lowest energy) and the least stable (highest energy) conformations. There is continuous rotation in ethane because 12 kJ/mol is a very low barrier, and at any time, approximately 99% of the ethane molecules are in a staggered conformation.
Here is also a short video clip for the conformational analysis of ethane:
Conformational Analysis of Propane
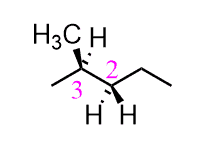
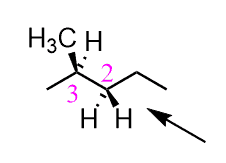
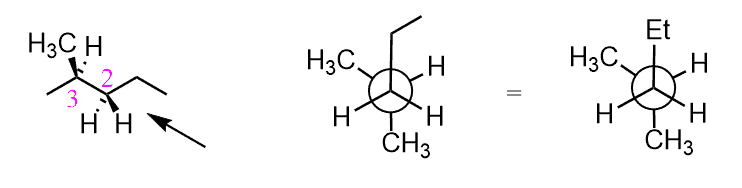
The same definitions and principles regarding conformational analysis apply to other alkanes; however, as they get larger, the repulsive interactions increase and the energy difference between different conformations becomes more significant. Propane has an extra carbon which replaces one of the hydrogens in ethane, and we will see in the Newman projection that in the eclipsed conformation, there are two eclipsing hydrogens and one H : CH3 eclipsing interaction.
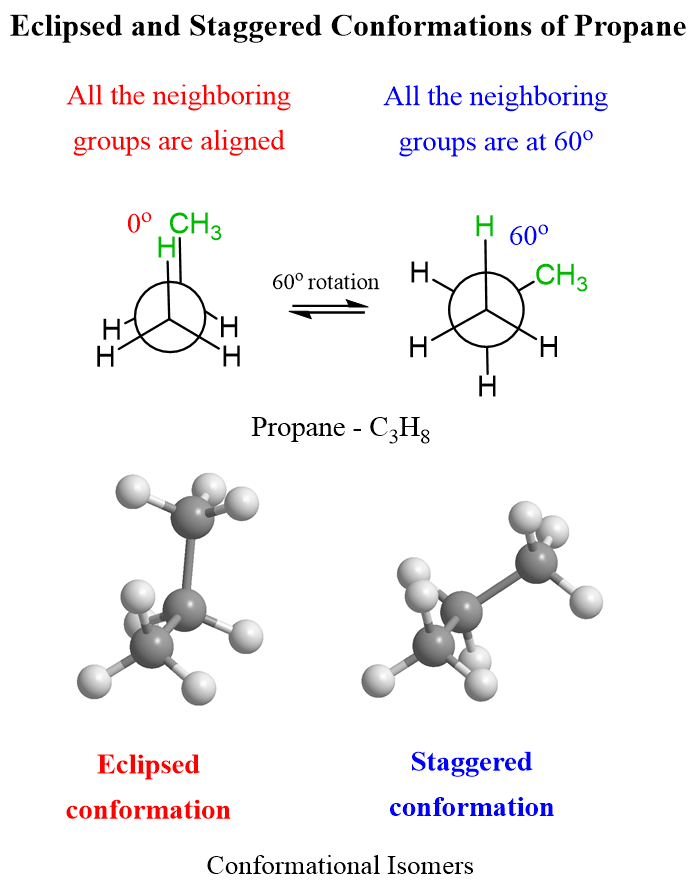
It has been shown that the energy barrier between the staggered and eclipsed conformations of propane is 14 kJ/mol (3.4 kcal/mol):

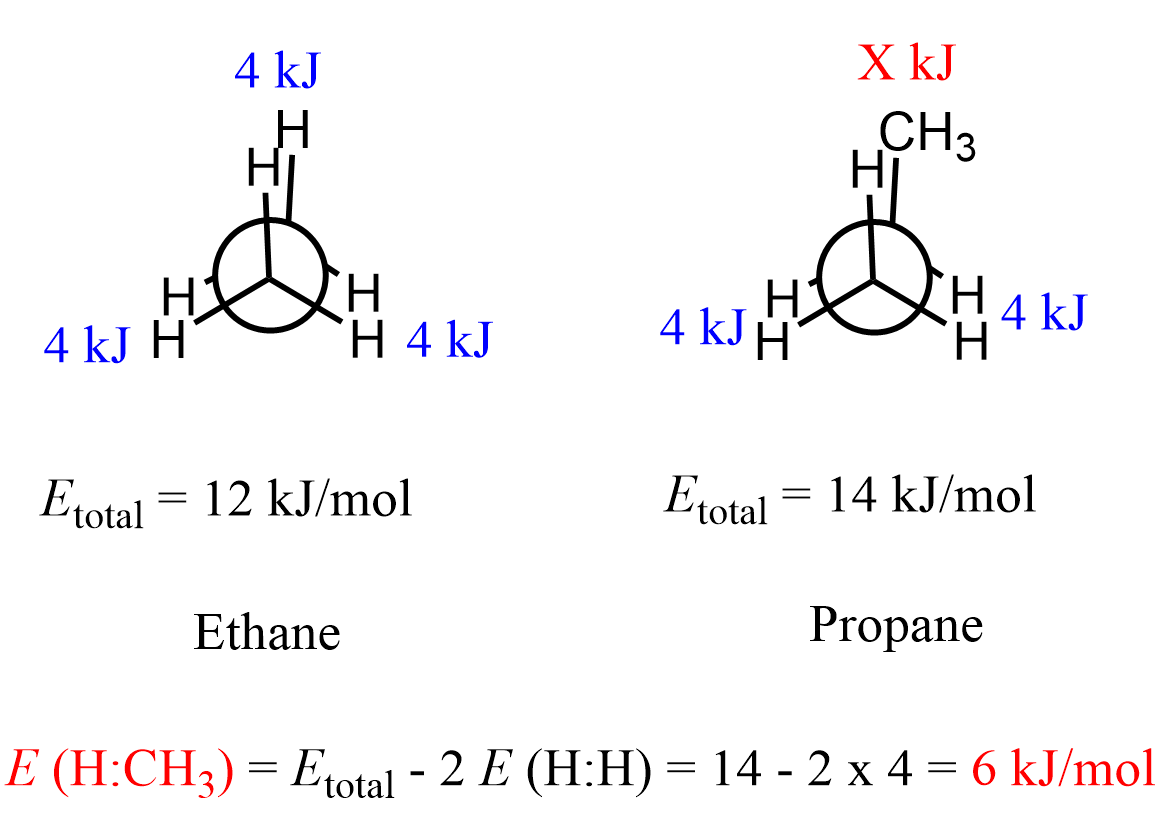
We could also calculate the energy of eclipsing H and CH3 groups, knowing the barrier to rotation for ethane (12 kJ/mol). This energy is due to three pairs of eclipsing hydrogens, and therefore, the energy of one pair of eclipsing hydrogens would be (12 kJ/mol ÷ 3 = 4 kJ/mol or about 1 kcal/mol).
Keeping this in mind, recall that propane has two pairs of eclipsing hydrogens and one H : CH3 interaction. Therefore, to find the energy of one eclipsing H : CH3 pair, we subtract the energy of two H : H interactions from the total energy gap (barrier to rotation) of propane:
Let’s also demonstrate the staggered and eclipsed conformation of propane together with the corresponding dihedral angles and energy values in a short video clip:
Conformational Analysis of Butane
The conformational analysis of butane is based on the different conformations achieved via the rotation of the C2-C3 bond.
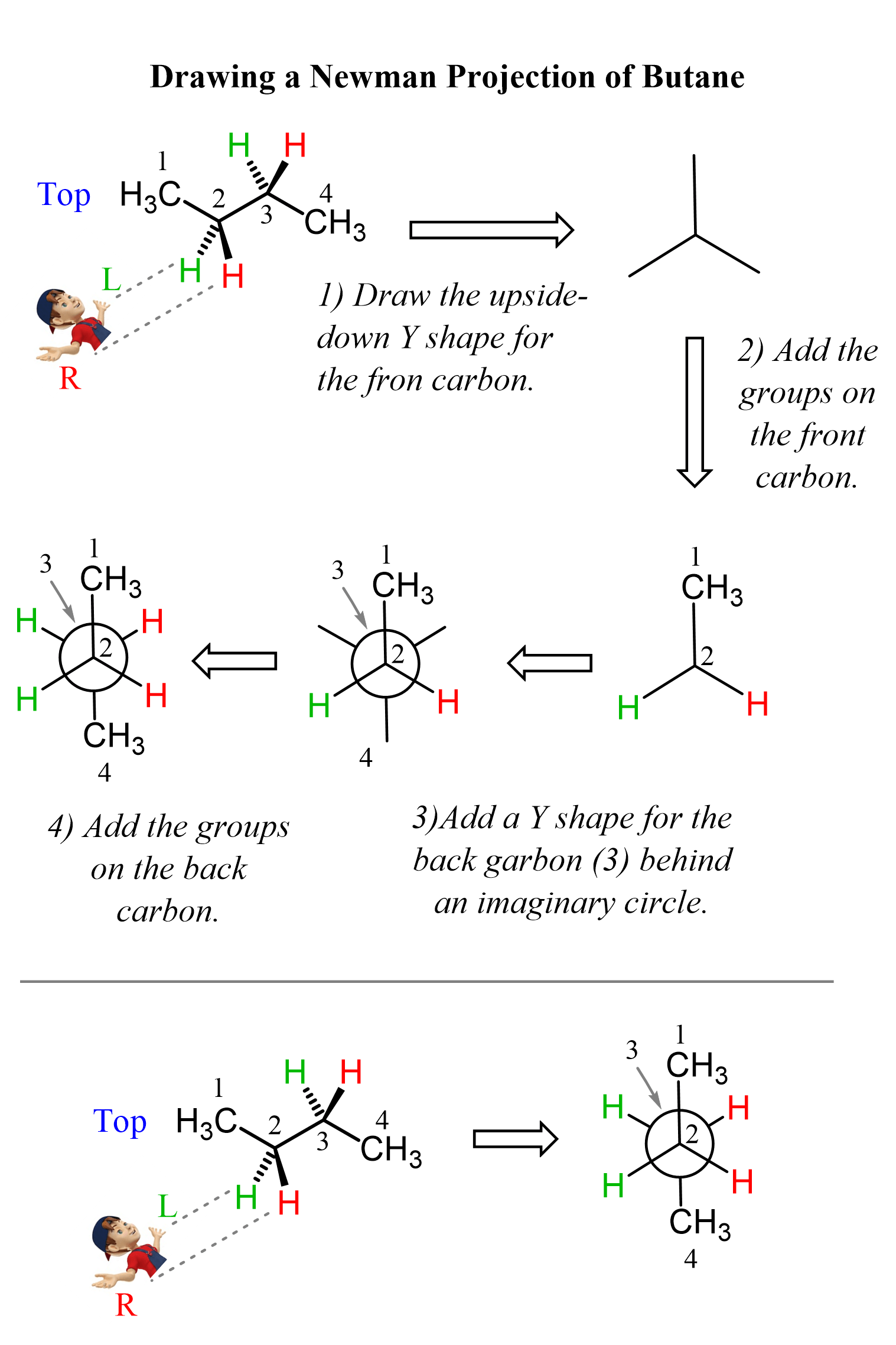
Unlike propane and ethane, the energy diagram of butane is a bit more complicated because there are two methyl groups, and steric interactions between them occur even when they are at 60o. These interactions are called gauche, and the corresponding conformations are known as gauche conformations. This is not referred to methyl groups only, other alkyl groups and halogens, for example, also have gauche interactions.
As a general representation, we can illustrate them as shown below:

Notice that when the largest groups are at 180o, the conformation is called anti, and when they are aligned (0o), we have a syn conformation. The anti conformation is the most stable, and the anti conformation is the least stable:

The gauche conformation is in the group of staggered conformations, but it is 3.8 kJ/mol higher than the anti conformation because of the steric interactions between the methyl groups. We have a separate post about the Newman projections and conformational analysis of butane, but as a summary, you can refer to the following short video clip for a better visualization:
Conformational Analysis of Cyclic Molecules
Cycloalkanes and other cyclic compounds with single bonds also have different conformations due to the possibility of rotations about single bonds. Like for simple alkane, not all the conformations of cyclic compounds are energetically equivalent.
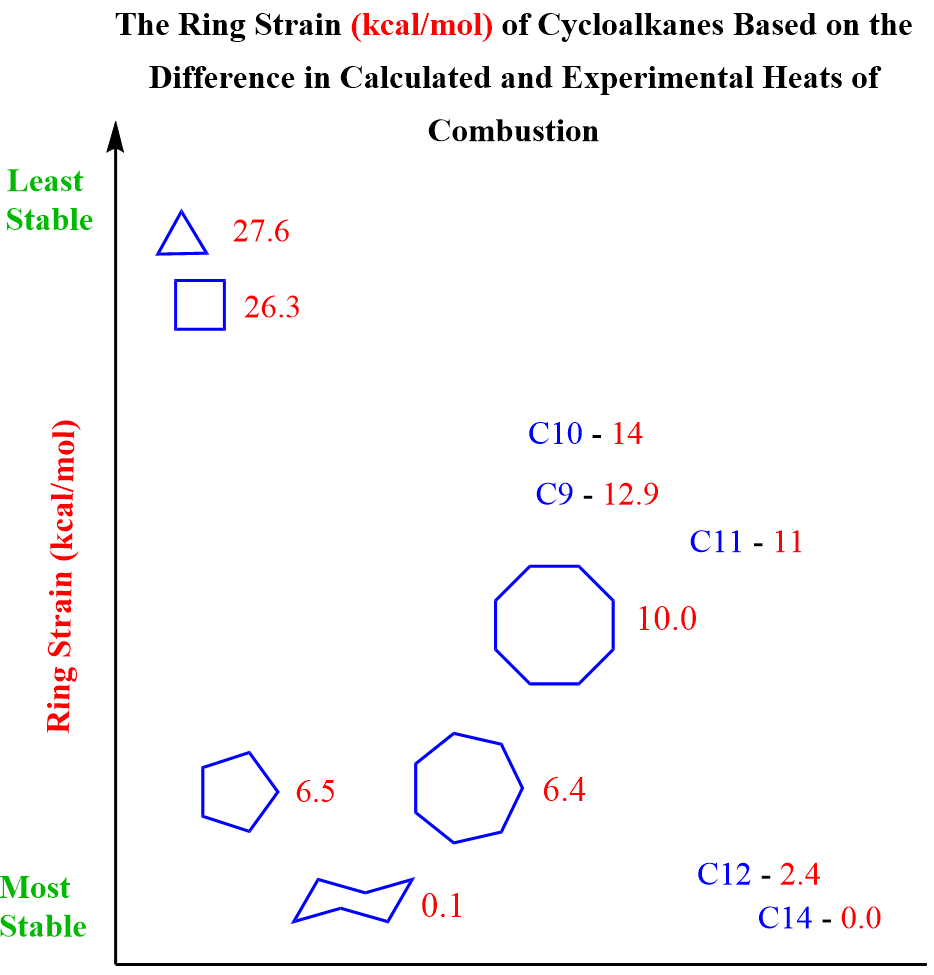
To discuss these conformations, let’s first mention that cycloalkanes are less stable than their corresponding alkanes. This instability is explained by what is called a ring strain. The ring strain is the combination of two destabilizing factors: angle strain and torsional strain.

- The angle strain rises because the bond angle in the ring is forced to change from the ideal 109.5o tetrahedral geometry.
- The torsional strain, as we discussed earlier, is due to the repulsive forces between the bonding electrons of eclipsed atoms.
Cyclopropane
For example, cyclopropane is the least stable cycloalkane because of great angle and torsional strain. The bond angles are 60o which gives the greatest deviation from the tetrahedral geometry. This yields poor orbital overlap and increases the energy of the molecule:
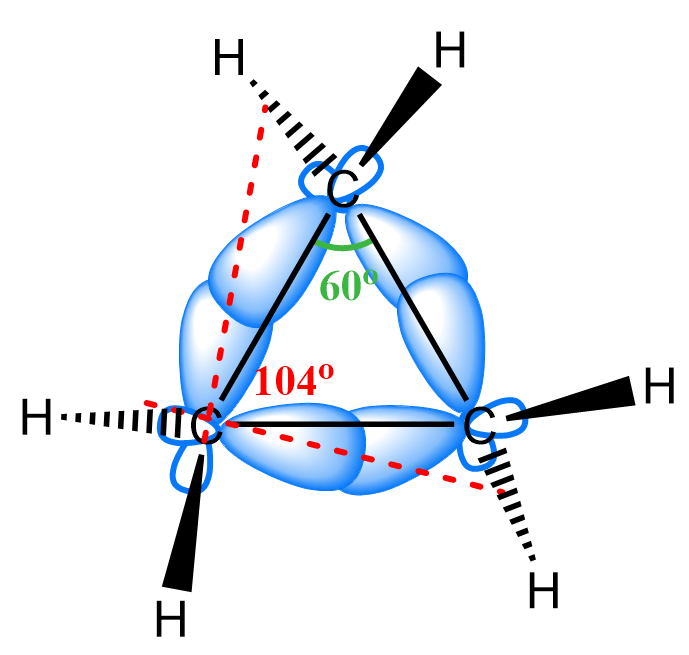
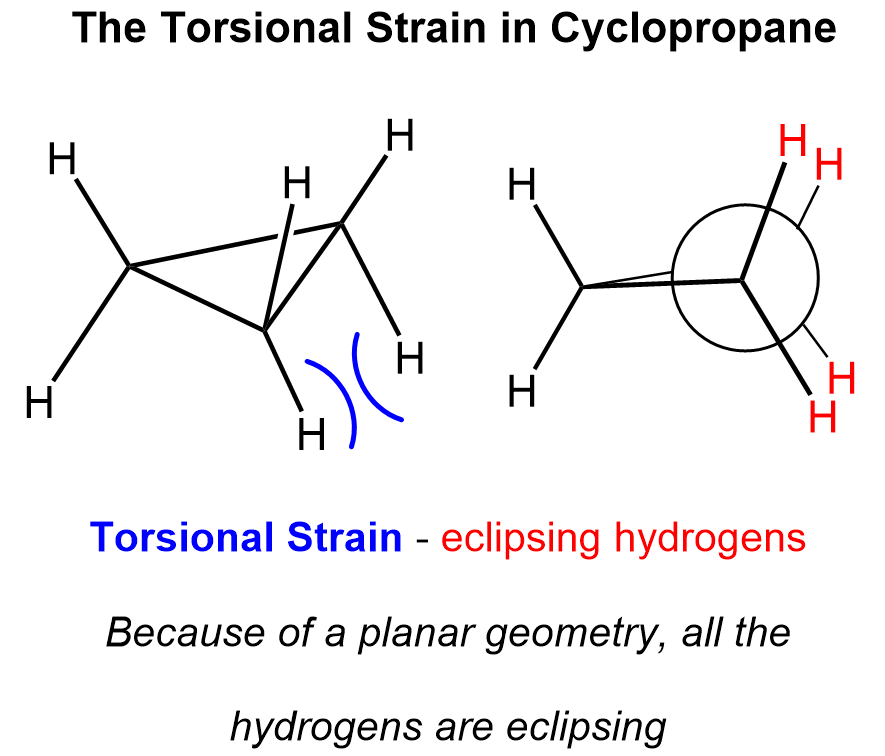
In addition, all the hydrogen atoms are eclipsed, and there is no other conformation that could allow avoiding this:
Let’s also see the eclipsing hydrogens in propane in a short video clip:
In other words, cyclopropane has only one conformation which is planar, and this geometry is energetically very unfavorable.
Cyclobutane
Cyclobutane, for example, avoids this high torsional strain by adopting what is called a puckered conformation. The trade for this is the smaller bond angle (88o), which is still energetically more favorable than having all the C-H bonds eclipsing:
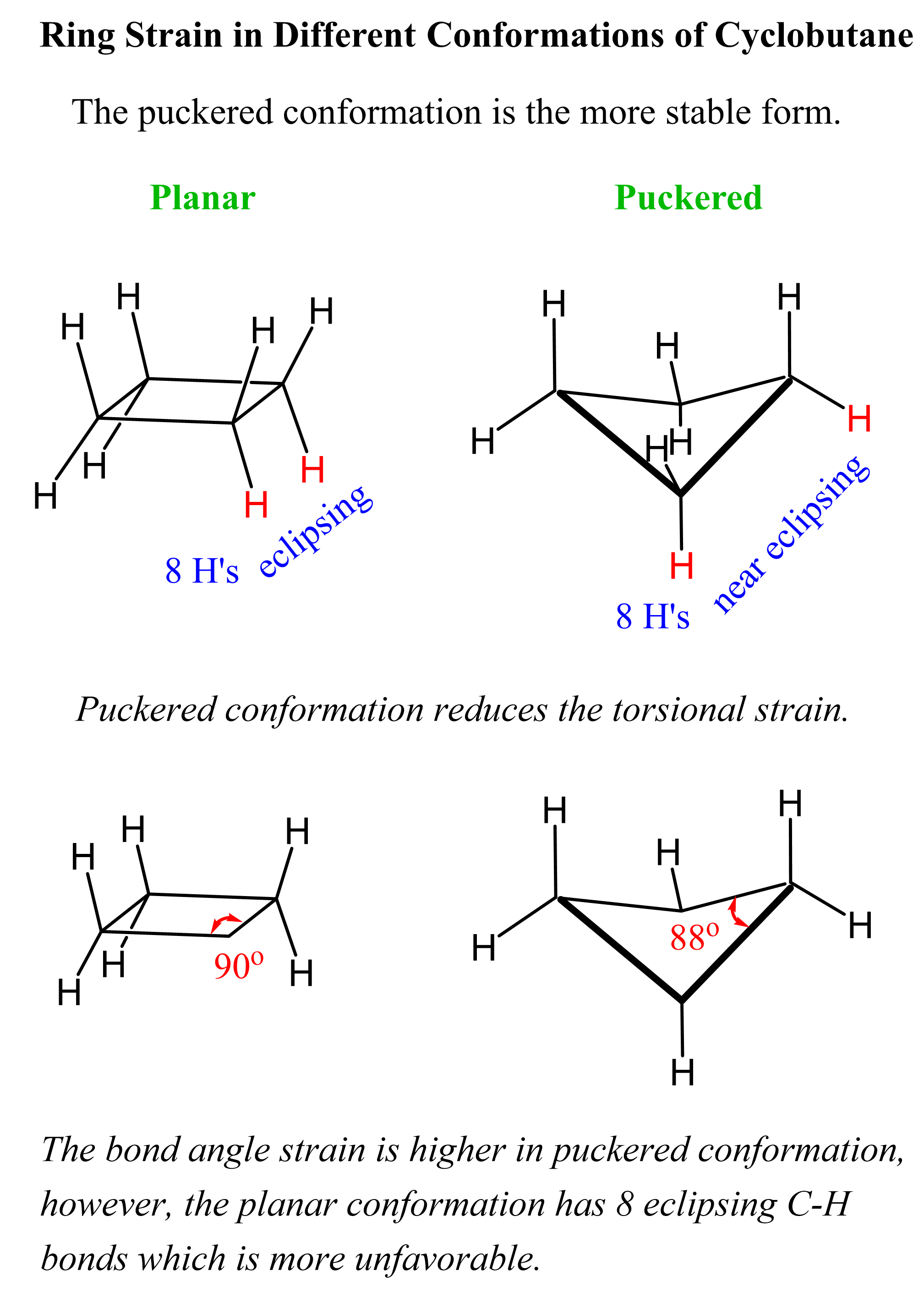
If cyclobutane were planar, there would be eight pairs of eclipsing hydrogens, making it to about 8 x 4 kJ/mol = 32 kJ/mol of torsional strain. In the puckered conformation, none of the hydrogens are completely eclipsed:
At any given time, the molecule exists as a mixture of different conformations, and cyclobutane has been shown to have a 110 kJ/mol of ring strain, which is slightly less than cyclopropane (115 kJ/mol).
Cyclopentane
The bond angle of a pentagon is 108o which is very close to the tetrahedral angle of 109.5o. Cyclopentane, however, is not planar because that conformation would result in 10 eclipsing C-H bonds. And, like cyclobutene, it assumes a slightly bent conformation commonly known as envelope conformation:
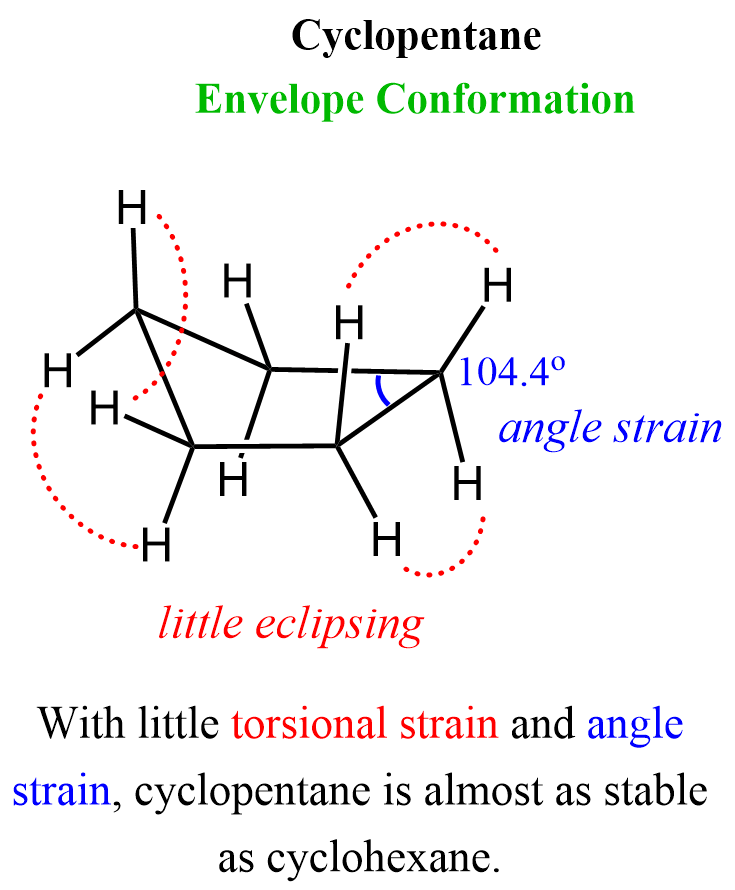
In this conformation, only the hydrogens in the right side of the image are near eclipsing:
These eclipsing hydrogens and the insignificant angle train give a little ring strain of 26 kJ/mol.
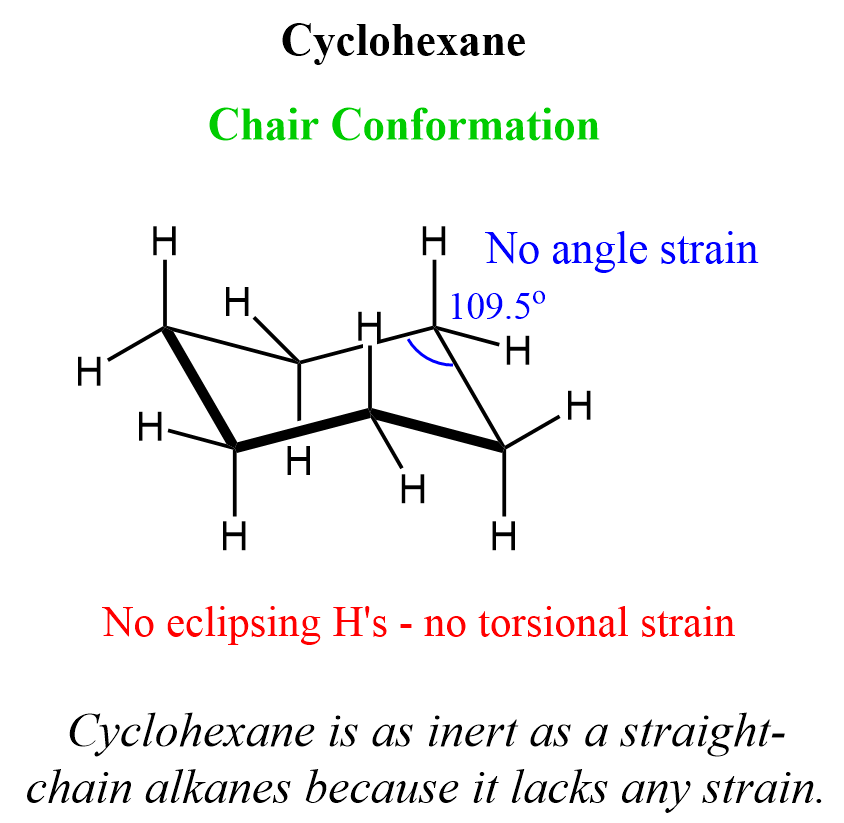
Cyclohexane
Cyclohexane is the most common ring structure found in many natural and synthetic structures. The main reason for this abundance is its great stability as it lacks any angle and torsional strain. This is achieved by adopting the most stable conformation known as the chair conformation. The chair conformation puts the carbon atoms at nearly ideal 109.5o tetrahedral angle (111.4o in some literature) and excludes any eclipsing hydrogen atoms:
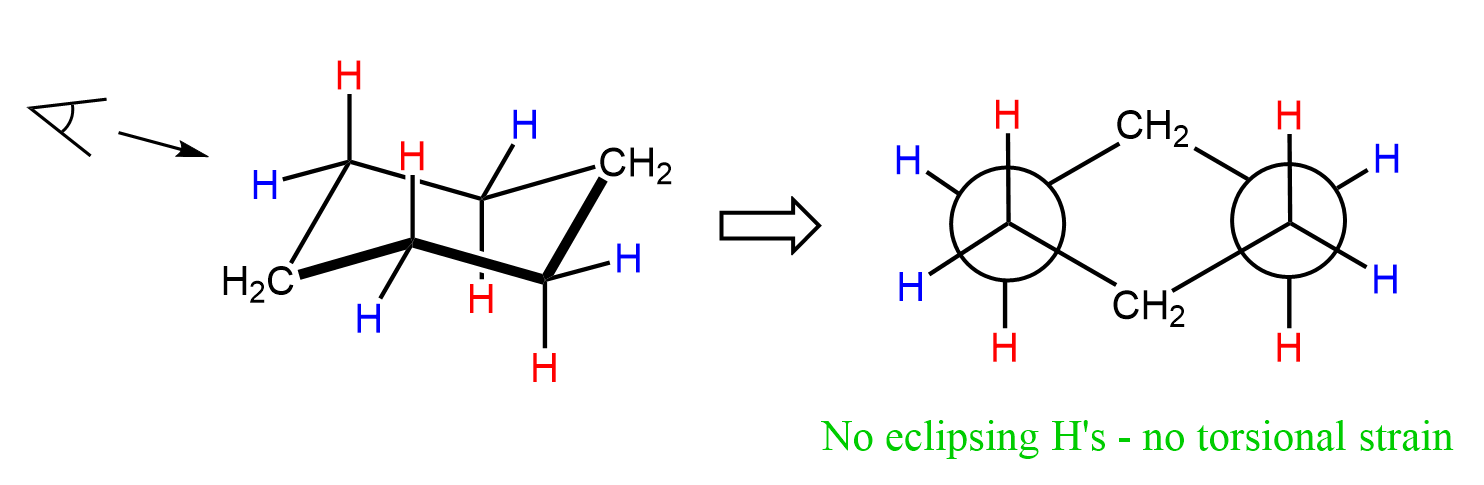
We can draw a Newman projection of cyclohexane in a chair conformation to confirm that the hydrogen atoms are maximally separated, thus lacking a torsional strain:
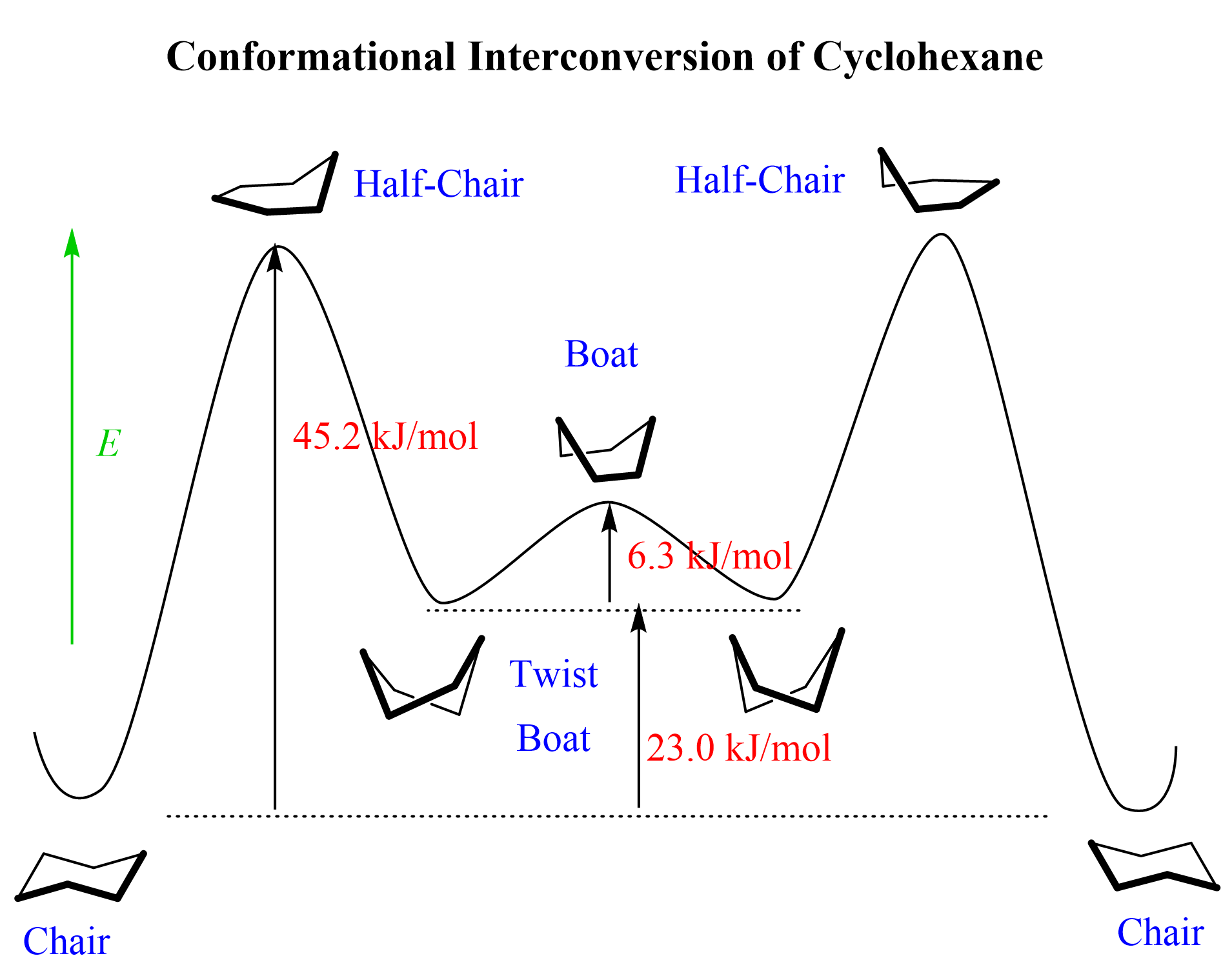
Cyclohexene undergoes an interconversion (ring flip) from one chair conformation to another via rotation about the C-C single bonds, and in between these chair forms, it passes through other, less stable, conformations known as the boat, half boat, and twist boat, and the ring flip passes via higher energy barriers to adopt these conformations:
The ring strain of these and other cycloalkanes is summarized in the following table, and for more details on how they are calculated, you can read “Ring Strain” post