In the previous post, we talked about the staggered and eclipsed conformations of ethane, and saw that these are the least and most stable conformations that differ by a 12 kJ/mol rotation barrier:
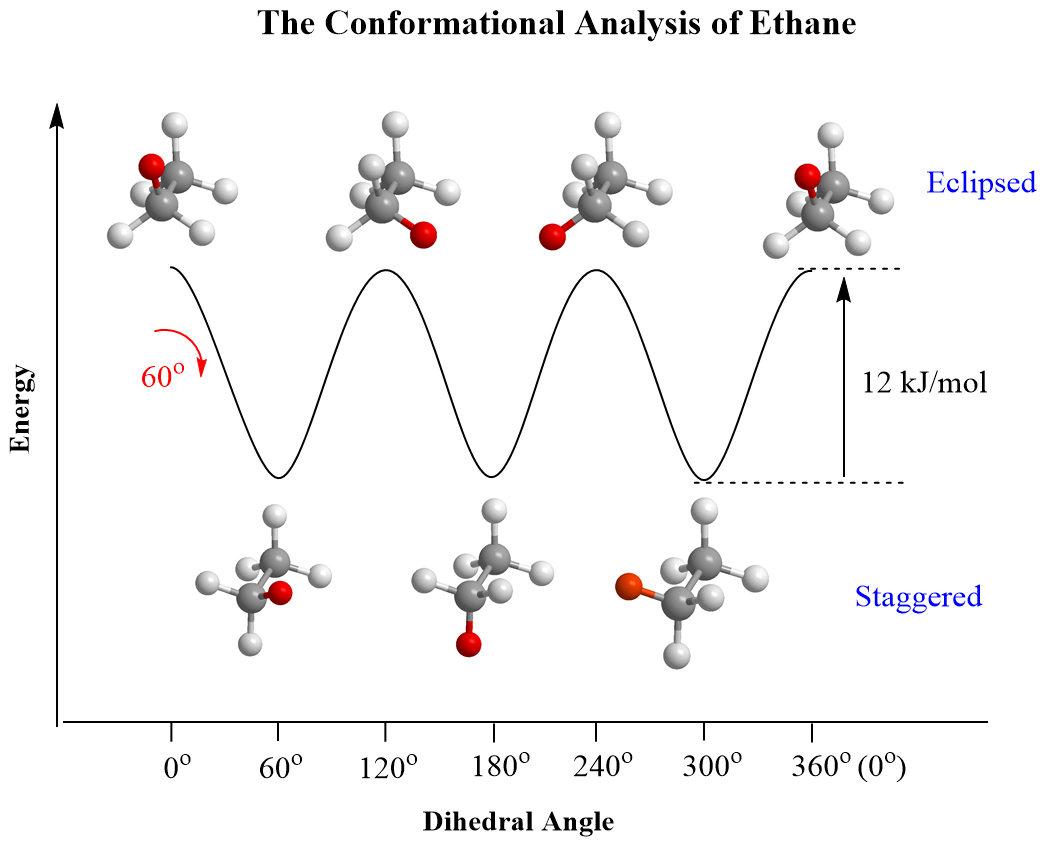
The staggered conformation is the most stable (lower in energy) and the eclipsed conformation is the least stable (higher in energy) due to repulsive interactions between the eclipsing hydrogen atoms. As a reminder, in eclipsed conformations, all the atoms on neighboring carbons are at 0o (dihedral angle), whereas in staggered conformations, the angle between them is 60o.

You can read the previous post on eclipsed and staggered conformations of ethane for more details here.
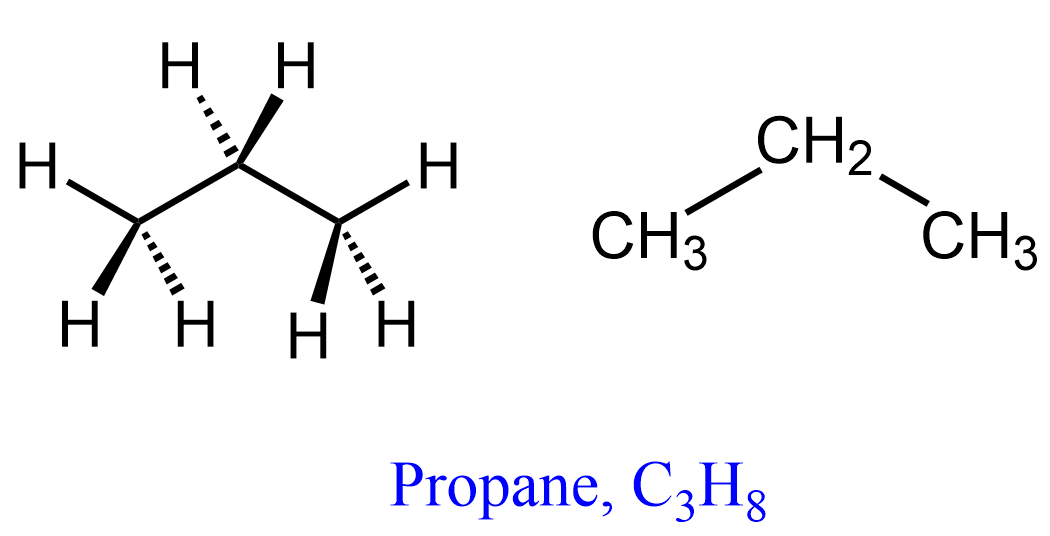
Now, the same definitions and principles regarding conformational analysis apply to other alkanes, however, as they get larger, the repulsive interactions are increasing and the energy difference between different conformations becomes more significant. Propane has an extra carbon which replaces one of the hydrogens in ethane, and we will see in the Newman projection that in the eclipsed conformation, there are two eclipsing hydrogens and one H:CH3 eclipsing interaction. So, first, let’s draw the wedge and dash representation of propane:
Next, we need to choose the direction to look from in order to draw the corresponding Newman projection. Remember, a molecule can have a number of Newman projections depending on along which bond we are looking. If drawn correctly, they are all valid representations just like any object can have multiple projections. So, let’s number the carbon atoms and look through the C1-C2 bond:
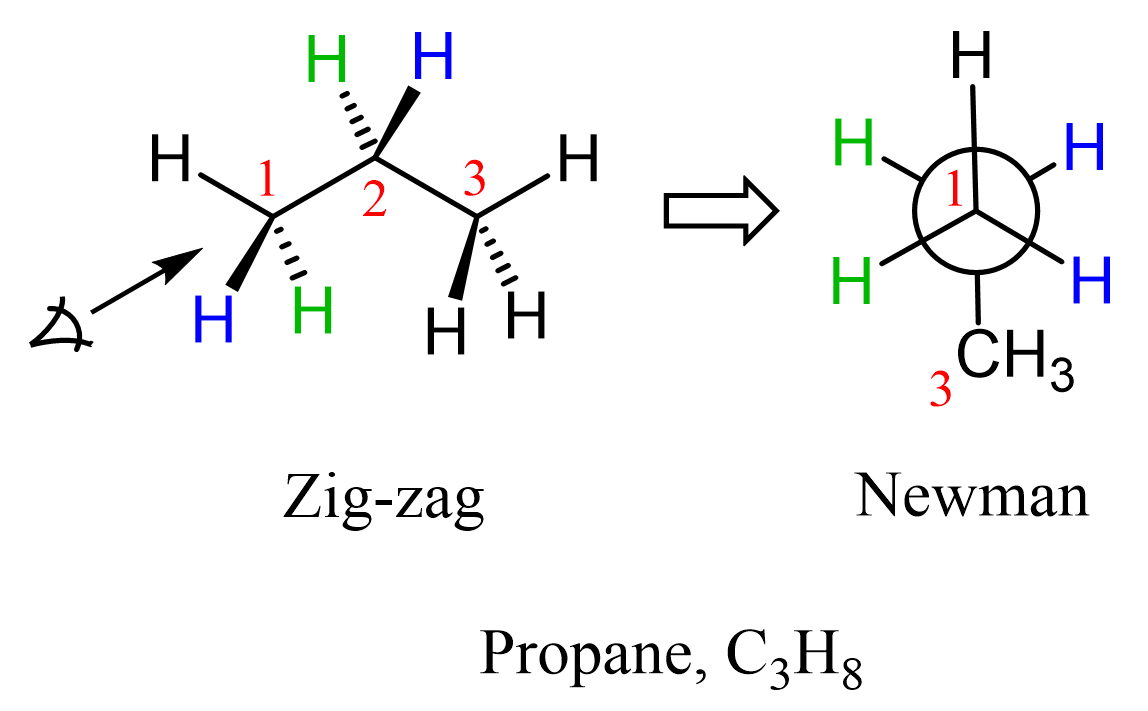
Carbon 1 is in the front, carbon 2 is in the back of the imaginary circle, and carbon 3 is the methyl group in a condensed form.
This is the (or one of the, to be more accurate) staggered conformation of propane as all the atoms/groups on neighboring carbons are at 60o. Let’s now draw the eclipsed conformation of propane. Remember, these conformations are interchanged via a 60o rotation about the C-C single bond. To emphasize the dihedral angle, we will color the methyl group and the corresponding hydrogen in green:
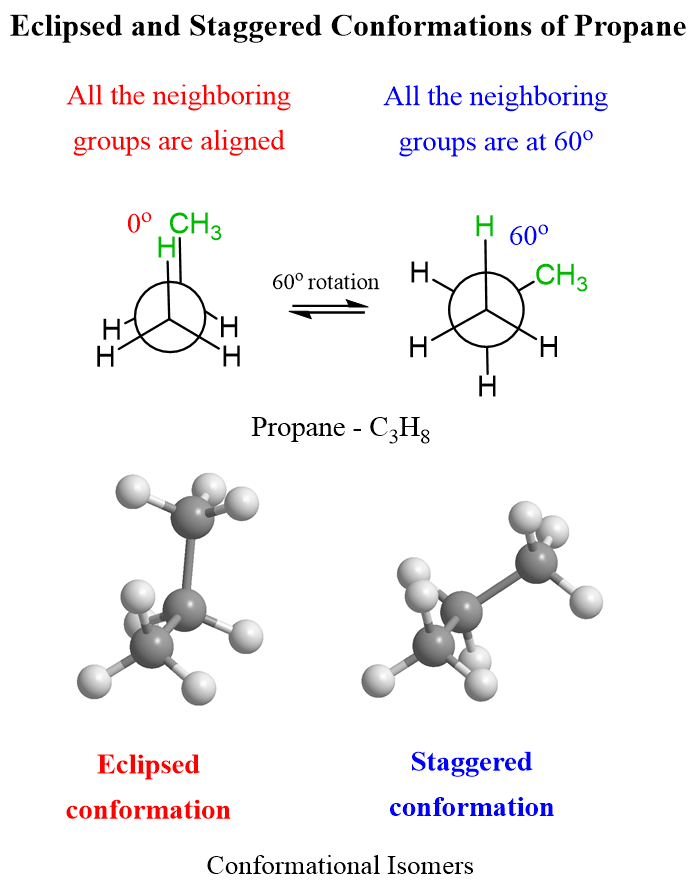
Conformational Analysis of Propane
Conformational analysis is the study of the relative stabilities of different confirmations of a molecule. It is important to mention that ethane and most other molecules where there are no restricted factors such as, for example, a double bond or large groups, exist in infinite number of conformations. This is because the rotation about all the single bonds is continues and happens thousands or millions of times in a second depending on the temperature, media, and structure of the molecule.
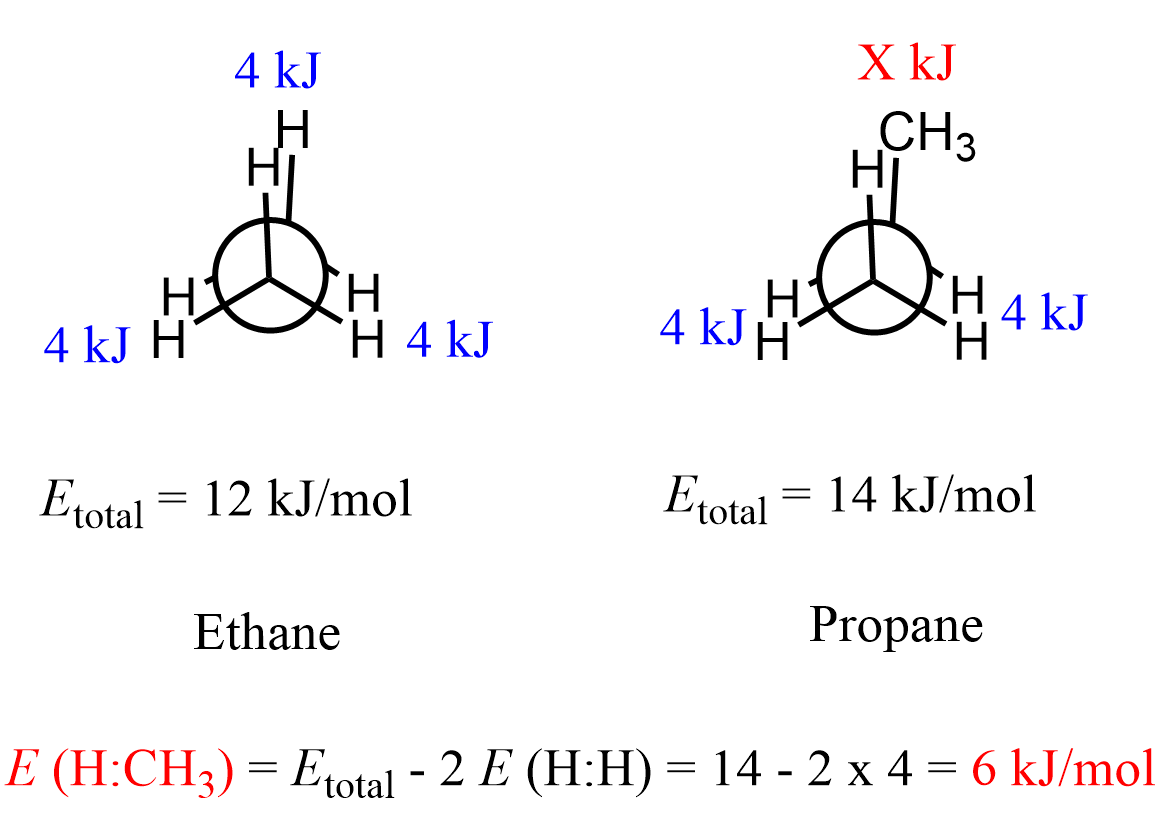
We only focus on the distinct/extreme conformations with the largest energy gaps because these are where the molecule spends the most and least amount of time, and thus they define its physical and chemical properties. These are the staggered and eclipsed conformations, and for propane, it has been shown that the energy barrier between them is 14 kJ/mol (3.4 kcal/mol):

This is slightly greater than the barrier to rotation in ethane (12 kJ/mol, 3.0 kcal/mol) because the methyl group (CH3) is larger than the hydrogen atom, and as a result, there is a greater steric interaction with the hydrogen on the neighboring carbon. The following table summarizes the torsional and steric energies of eclipsing groups as well as those of gauche interactions which we will discuss in a separate article:

Although quite similar and often used interchangeably, the steric torsional interactions have different definitions. Stericsor steric interactions are the obstructions caused by the size of neighboring groups and atoms. Torsional interactions are the result of repulsive forces between the bonding electrons of neighboring atoms. Because of the small size of hydrogen, the H:H and H:CH3 interactions are considered be mainly torsional, whereas two methyl groups get on each other’s way and the steric factor is more significant.
Now, suppose we did not have this data. We could still calculate the energy of eclipsing H and CH3 groups knowing the barrier to rotation for ethane (12 kJ/mol). This energy is due to three pairs of eclipsing hydrogens, and therefore, the energy of one pair of eclipsing hydrogens would be (12 kJ/mol ÷ 3 = 4 kJ/mol or about 1 kcal/mol).
Keeping this in mind, recall that propane has two pairs of eclipsing hydrogens and one H:CH3 interaction. Therefore, to find the energy of one eclipsing H:CH3 pair, we subtract the energy of two H:H interactions from the total energy gap (barrier to rotation) of propane:
Let’s also demonstrate the staggered and eclipsed conformation of propane together with the corresponding dihedral angles and energy values in a short video clip:
Check Also
- Naming Alkanes by IUPAC nomenclature Rules Practice Problems
- Naming Bicyclic Compounds
- Naming Bicyclic Compounds-Practice Problems
- How to Name a Compound with Multiple Functional Groups
- Primary Secondary and Tertiary Carbon Atoms in Organic Chemistry
- Constitutional or Structural Isomers with Practice Problems
- Degrees of Unsaturation or Index of Hydrogen Deficiency
- The Wedge and Dash Representation
- Sawhorse Projections
- Newman Projections with Practice Problems
- Gauche Conformation, Steric, Torsional Strain Energy Practice Problems
- Staggered and Eclipsed Conformations
- Ring Strain
- Drawing the Chair Conformation of Cyclohexane
- Ring Flip: Drawing Both Chair Conformations with Practice Problems
- 1,3-Diaxial Interactions and A value for Cyclohexanes
- Ring-Flip: Comparing the Stability of Chair Conformations with Practice Problems
- Cis and Trans Decalin
- IUPAC Nomenclature Practice Problems
- IUPAC Nomenclature Summary Quiz
- Alkanes and Cycloalkanes Practice Quiz
